どうもこんにちは,Megです.
以下の論文のサーベイメモをまとめていきます.
フォーマットは「Chem-Station,”研究者目線からの論文読解を促す抄録フォーマット”,2017.」を参考にさせていただきました.
論文内容における解釈違いの可能性があることをご容赦ください…!
サーベイ論文
佐久間一輝, 森田純哉, 平山高嗣, 榎堀優, 間瀬健二. 脳波を対象とした深層ニューラルネットの可視化による構造発見. 人工知能学会全国大会論文集. 2020, vol. JSAI2020, p. 1I5GS202-1I5GS202.
研究の概要
脳波(EEG)分析では,専門家の高度な技術によりノイズ除去や結果の解釈がなされてきた.
一方,深層学習(DNN:Deep Neural Network)の可視化手法は,特徴抽出が意図したものかを確認するために用いられる.
本研究では,DNNの識別精度毎のモデル可視化結果を比較することで,任意の現象固有の構造を抽出する手段を検討した.
実験ではEEGから事象関連脳電位(ERP)を識別する学習を行い,モデルの可視化分析から既知の特徴的な構造が得られた.
問題設定と解決した点
問題点
DNNは,モデルの内部でどのように特徴量を抽出しているか理解し難い.ゆえに,実社会においてDNNの利用が制限されている.
一方で,XAI技術の研究は進められているが,DNNが意図した特徴量を抽出できているかを確認することにとどまり,分類対象を分析することは考慮されていない.
解決策
これらの背景を踏まえて,本研究では,前提としてEEGを対象としたDNN出力の分散を仮定する.上位の識別精度を有するDNNモデルを検討することで,EEGに内在する構造を発見する新手法を提案する.
技術や手法のキモ
実験データ
本実験では,BCI Competition Ⅲ Data2を使用した.
このデータはP300 spellerという文字入力インターフェースが使用される.スクリーン上のマトリックスがランダムに光り,意図した文字が点灯した際にP300が生じ,それをP300 spellerで検出する.
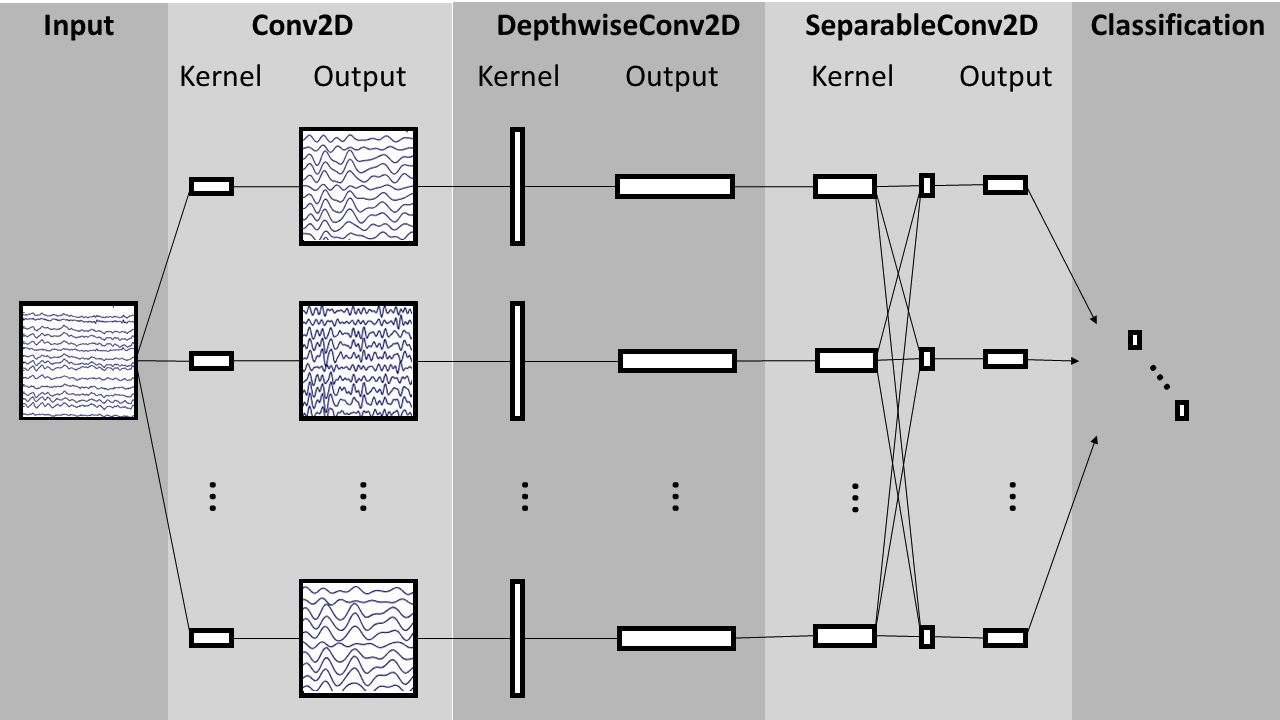
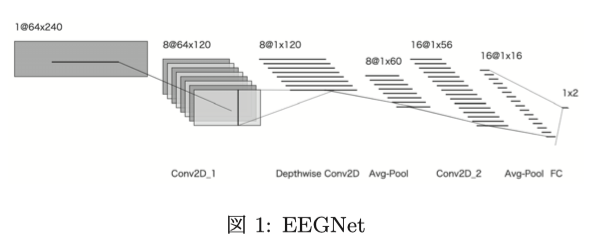
EEGNet
EEGを識別するDNNとしてEEGNetがある.EEGNetはBCIに特化した軽量なDNNであり,少ない学習データで学習できる.加えて,様々なBCIタスクに適用可能であるという利点がある.
教師ラベルは意図した文字にチア王する刺激が提示されたかどうかの2クラス分類とした.
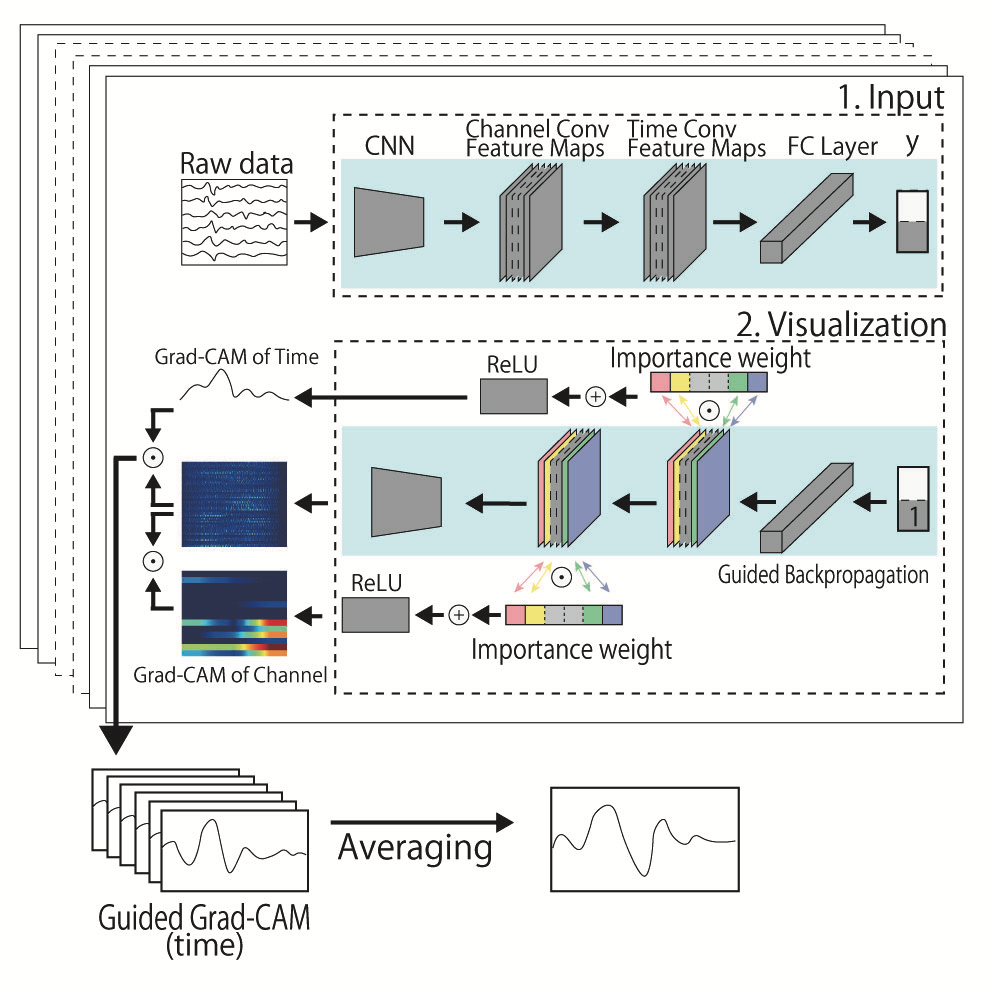
Guided Grad-CAM
可視化分析には,Grad-CAMとGuided Backpropagationを組み合わせたGuided Grad-CAM(GGC)を使用した.
本研究でのEEGNetは,Conv2D_1層とConv2D_2層で時間軸,DepthwiseConv2D層でChannel軸で畳み込みを行っており,時間軸で畳み込んでいる層により出力された特徴マップを使用し,P300を取得する一連の実験でどの時間帯の注目度が高いかを可視化した.
EEGとGGCを用いた中間層の可視化と集約の手法の概念を図4に示した.
有効性の検証
DNNの分散を生じさせる要因
DNNの認識精度において,分散を生じさせる要因として,
- K-Fold(経験的要因)
- データの提示順(経験的要因)
- 初期値乱数を変化(生得的要因)
の3つを上記のように生得的要因と経験的要因として仮定し,DNNの識別精度に対して生得的要因と経験的要因がどの程度影響するかを検証した.
下記の表と図が結果である.
| Fold1 | Fold2 | Fold3 | Fold4 | Fold5 | |
|---|---|---|---|---|---|
| 識別精度の平均 | 0.714 | 0.716 | 0.696 | 0.688 | 0.697 |
| 識別精度の分散 | 0.0195 | 0.0191 | 0.0241 | 0.0178 | 0.0190 |
以降の実験では,平均認識精度が高いFoldを用いて分析した.
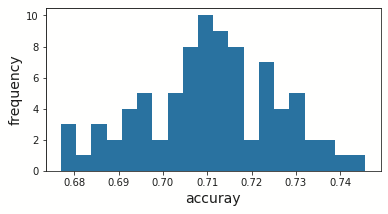
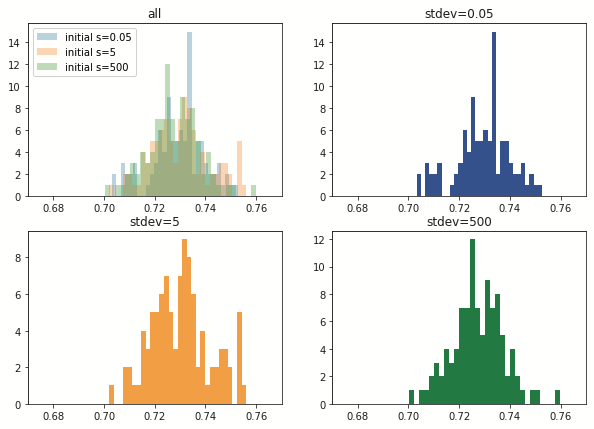
Fold間(経験的要因)の結果から,学習に用いるデータごとに識別精度の分散が異なった.
初期値乱数を変化(生得的要因のみ)させた際の識別精度の標準偏差は,約0.0114であった.
使用データを固定(生得的要因+経験的要因)した際の識別精度の標準偏差は,0.0152であった.
| 実験名 | 使用データ | データの提示順 | 初期値乱数の標準偏差 | 識別精度の分散 |
|---|---|---|---|---|
| 実験2 | 実験3と同様 | ランダム | 固定 | 0.0152 |
| 実験3 | 実験2と同様 | 固定 | 変化 | 約0.0114 |
これらよりデータを与える順番(経験的要因)により,標準偏差に約0.004の差が生じていると言える.
以上より,DNNの初期値(生得的要因)と学習データ(経験的要因)はともに識別精度の標準偏差に影響を与えることが明らかになった.ゆえに,生得的要因・経験的要因を用いた心理学的アプローチをDNNに対して行うことができると考える.
可視化結果の分析
初期値分散を固定した各モデルに対してGGCを用いて,各時刻におけるDNNの注目度を波形として可視化した.識別精度が高かった5つのモデルの可視化結果を図5,識別精度が低かった5つのモデルの可視化結果を図6に示した.
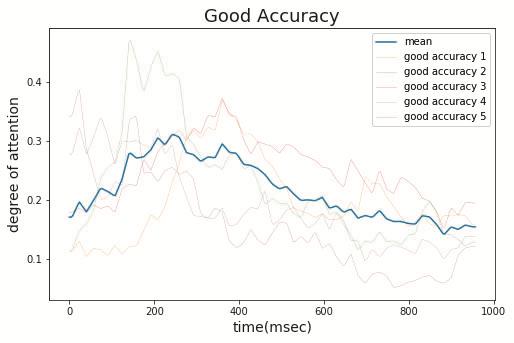
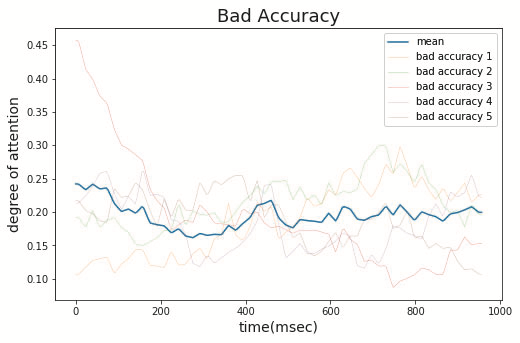
図5から,識別精度が高いものは300ms付近に注目していることがわかる.対して,図6から,識別精度が低いものは300msに注目していないことがわかる.
よって,識別精度の高いDNNはP300を観測し区別するための内容を捉えているといえる.
議論・結論
本研究では,
- 学習データの提示順・DNNの初期値は学習結果に影響することがわかった.
- 識別精度の高いDNNはP300の構造と本質を捉えていたと考えられる.
これまで,DNNの識別精度の分散は注目されてこなかったが,分散を仮定することで,心理実験的なアプローチを適用でき,DNNの理解を深める1つの手段になることを示唆する.
次に読むべき論文
吉田蒼生, 佐藤輝, 石川文之進, 加我君孝, 深見忠典. EEGNetを用いた応答に対する加重平均処理による事象関連電位計測時間の短縮. 生体医工学. 2021, vol. Annual59, no. Abstract, p. 486–486.
本実験と同様に,ERPデータに対してEEGNetを使用している.計測時間を目的としているため,アーキテクチャ面で参考にできるところがあるかも.
参考文献
EEGNet
Lawhern, Vernon J., Solon, Amelia J., Waytowich, Nicholas R., Gordon, Stephen M., Hung, Chou P., Lance, Brent J. EEGNet: a compact convolutional neural network for EEG-based brain–computer interfaces. Journal of Neural Engineering. 2018, vol. 15, no. 5, p. 056013.
Guided Grad-CAM
Selvaraju, Ramprasaath R., Cogswell, Michael, Das, Abhishek, Vedantam, Ramakrishna, Parikh, Devi, Batra, Dhruv. Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization. International Journal of Computer Vision. 2020, vol. 128, no. 2, p. 336–359.
ERP P300
(1) Polich, John. Updating P300: An Integrative Theory of P3a and P3b. Clinical neurophysiology : official journal of the International Federation of Clinical Neurophysiology. 2007, vol. 118, no. 10, p. 2128–2148.